Why Qubit Layout Should Be Considered when Designing Quantum Circuits

As quantum computing continues to advance, the architecture of quantum processing units (QPUs) is becoming increasingly critical to the performance of quantum circuits, the backbone of all quantum algorithms. A key factor influencing the design of these circuits is qubit connectivity—how qubits are arranged and interact within a QPU. Different quantum platforms exhibit unique connectivity patterns that directly impact how quantum circuits are implemented and optimized.

In this post, we explore how qubit connectivity patterns shape circuit design and influence performance across various quantum architectures, including superconducting qubits, trapped ions, photonic qubits, and neutral atom qubits. To illustrate these concepts, we present a specific example involving the encoded Grover’s search algorithm, demonstrating how different connectivity models necessitate tailored approaches to circuit design for optimal performance. We highlight the significance of qubit layout in superconducting quantum computers on the Helmi QPU. Thoughtful consideration of QPU qubit layout in circuit design can lead to significant performance improvements.

Qubit Connectivity Across Different Quantum Architectures

Different quantum computer implementations, such as superconducting qubits, trapped ions, and photonic qubits, each have unique qubit connectivity patterns. This connectivity, or topology, refers to how qubits are physically arranged and how they can interact with one another. The nature of this connectivity directly impacts how quantum circuits are designed and executed.

1. Superconducting Qubits:

   Superconducting quantum computers typically arrange qubits in a 2D grid pattern on a chip, where each qubit interacts with its nearest neighbors, forming a lattice-like connectivity [1]. The strength of the interaction, or coupling, between qubits is largely determined by their physical proximity. The grid layout requires careful circuit design to minimize the need for long-range interactions, which require additional operations such as SWAP gates to bring qubits virtually closer together. Superconducting qubits are controlled using microwave electronics and pulse shaping techniques [2]. These qubits are, however, prone to imperfections such as decoherence, crosstalk, and leakage to non-computational states [3]. Circuit designs must therefore optimize qubit placement and operation sequences to mitigate these imperfections, aiming to reduce circuit depth and improve overall performance.

   

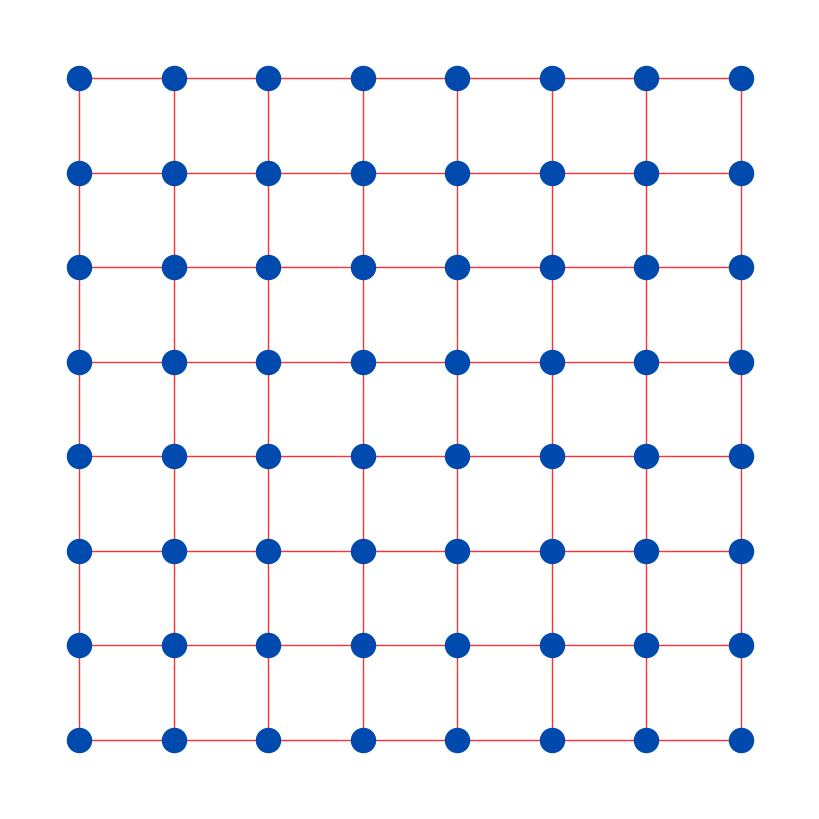
   Figure 1. 2D-grid connectivity graph, the blue dots represent qubits

2. Trapped Ion Qubits:

   In trapped ion quantum computers, the ions that form the qubits are often arranged in a linear or two-dimensional chain [4]. Any qubit in a trapped ion system can, in theory, interact with any other qubit, offering all-to-all connectivity [5]. This flexibility reduces the need for SWAP gates, potentially lowering circuit complexity. However, trapped ion systems are susceptible to readout bit flips, shuttling errors, and charge noise. Effective circuit design must manage these imperfections by ensuring robust control signals and maintaining qubit coherence over long ion chains to fully exploit the flexibility offered by this architecture [6].

   

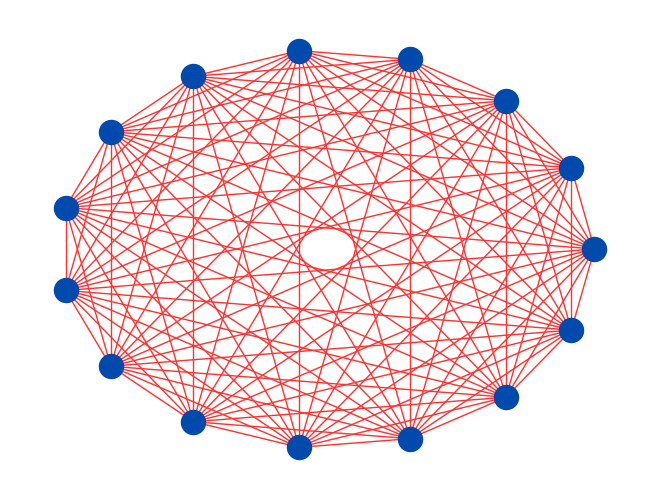
   Figure 2. All-to-all connectivity graph, the blue dots represent qubits

3. Photonic Qubits:

   Photonic quantum computers use light particles, photons, as qubits. Unlike other qubit systems, photonic qubits are not confined to a fixed spatial arrangement. Instead, they are typically guided through optical circuits using waveguides or fibers. The connectivity in photonic systems is determined by the design of these optical paths and components, such as beam splitters, waveplates, and phase shifters, which direct and manipulate the photons. This brings the advantages of long-distance quantum communication with excellent coherence time, while challenges such as optical loss, stray photons, and static fabrication defects must be addressed [7, 8, 9].

4. Neutral Atom Qubits:

   Neutral-atom quantum computers arrange individual atoms, their qubits, in 2D or 3D arrays, that can be dynamically reconfigured [10]. These atoms are typically manipulated and controlled using focused laser beams, known as optical tweezers, which trap and move the atoms to desired locations within the array. The interactions between qubits are controlled by adjusting the laser fields to induce interactions such as Rydberg states. This flexibility in control is advantageous for optimizing qubit interactions in real-time to meet specific circuit requirements. However, the neutral atom systems are prone to issues such as imperfect readout, qubit re-trapping, and shot-to-shot control variance from atomic motion [11].

Why Qubit Layout Matters in Superconducting Quantum Circuit Design

1. Optimizing Gate Implementation:

   The layout of a QPU directly affects how quantum gates, especially multi-qubit gates, are implemented. In superconducting quantum circuit, the qubit layout must be carefully planned to minimize the need for SWAP gates. SWAP gates, necessary for repositioning qubits to interact, increase the circuit depth and introduce additional sources of error. By optimizing the layout to align with the natural connectivity of the qubits, the number of SWAP operations can be significantly reduced, thus improving the overall fidelity and efficiency of the quantum computation. Even in architectures with more flexible connectivity, such as trapped ions, optimizing the layout can reduce latency and improve gate execution times.

2. Enhancing Scalability:

   As quantum computers grow in size and complexity, maintaining efficient and scalable circuit designs becomes increasingly challenging. The qubit layout must support the scaling of the system without a corresponding increase in error rates or operational complexity.

3. Supporting Quantum Error Correction:

   Quantum error correction (QEC) is important for achieving fault tolerance in large-scale quantum computers. Effective QEC codes, such as the surface code which has a low error threshold, require specific qubit arrangements, typically a 2D grid with nearest interactions. This layout supports the implementation of stablizer measurement which is used for error detecting and correcting. Therefore, the physical qubit layout should be designed to facilitate these measurements while minimizing the additional overhead from, for example, SWAP gates. Considering the qubit layout in the circuit design ensures the circuit is well-prepared to implement fault-tolerant operations.

4. Beyond Fault Tolerance: The Importance of Topology

   While fault tolerance has been a major focus in the development of quantum circuits, it is equally important to consider the physical topology of qubits, especially given the current state of quantum technology. In today’s Noisy Intermediate-Scale Quantum (NISQ) devices, with limited coherence times and non-negligible noise levels, optimization based on qubit topology can significantly improve circuit performance even before error correction is applied. By carefully designing the qubit topology, researchers can enhance the performance of quantum circuits, maximizing their capability before the implementation of full error correction. This consideration is not just about preparing for future fault-tolerant quantum computers but also about extracting the maximum potential from the quantum systems we have today.

Experiment: Comparing Circuit Design with Different Layouts

This experiment explores the impact of qubit layout on the performance of two implementations of the encoded Grover’s search algorithm. Although both circuits perform the same logical function, that is, they are mathematically equivalent, they differ in their encoding and decoding stages. This results in variations in the analysis stage to match the encoded outcome with the logical input. More details about how this encoded version of Grover’s search is implemented can be found here.

Encoded Version 1 (Figure 3) is based on the work by Pokharel and Lidar [12], but employs a different encoding method that better matches the star-shape topology of Helmi, our 5-qubit QPU. The original circuit for a linear chain topology (Figure 4) is here marked as Encoded Version 2. Circuit 1, which considers the actual topology of the QPU used, reduces the need for SWAP gates when running on Helmi.

Figure 3. Circuit 1 encoded with a star-shaped layout.

Figure 4. Circuit 2 encoded with a linear chain layout.

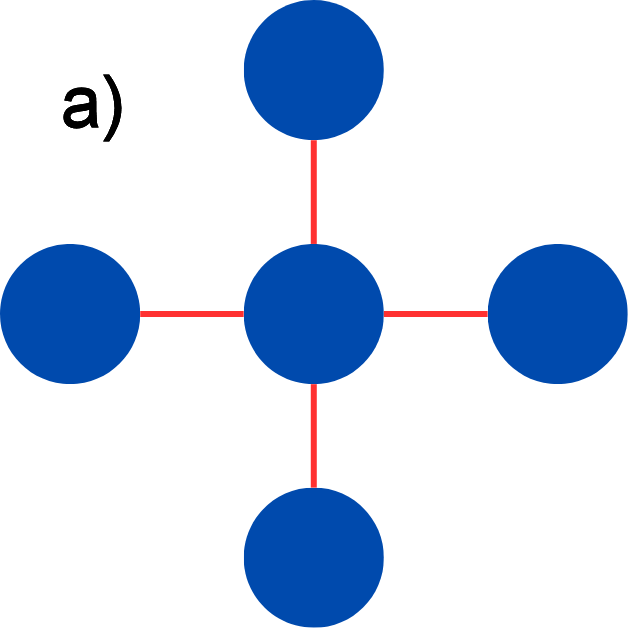
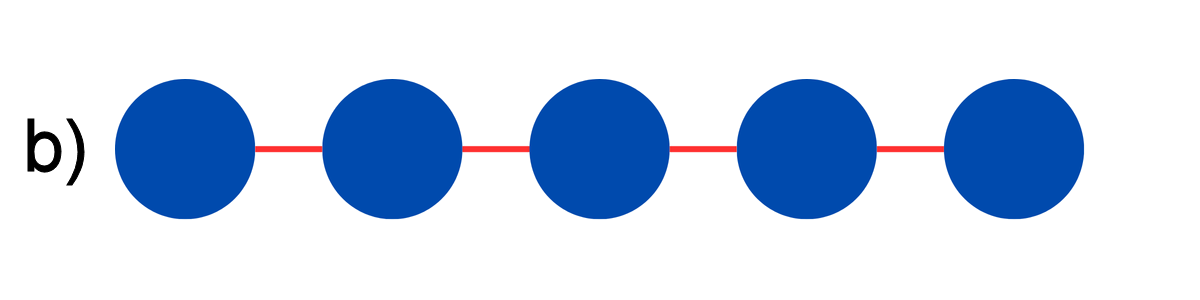
Figure 5. Different qubit layouts: a) star-shaped topology; b) linear-chain topology.

Table 1 shows the marked states (inputs) for the Grover’s search algorithm and their corresponding outputs for each version of the circuit. The marked state is the state that Grover’s algorithm is designed to find, and the outputs shown are the correct measurement outcome on data qubits after running the algorithm.

Table 1. Oracle marked state with corresponding correct output for the two versions of encoding.

Marked State (input)		00	01	10	11
Output	Version 1	0000	0011	0101	0110
	Version 2	0000	0010	0111	0101

Experiment Result

When these circuits were run on our 5-qubit QPU, Circuit 1 outperformed Circuit 2, demonstrating greater efficiency due to the layout-optimized design. The transpiled circuit depths of Circuits 1 and 2 are 29 and 54, respectively. This highlights how the same logical circuit can yield different results depending on how well the physical qubit layout matches the hardware’s connectivity. On average, Version 1 of the circuit performs 1.6 times better than Version 2, as seen in Figures 6 and 7.

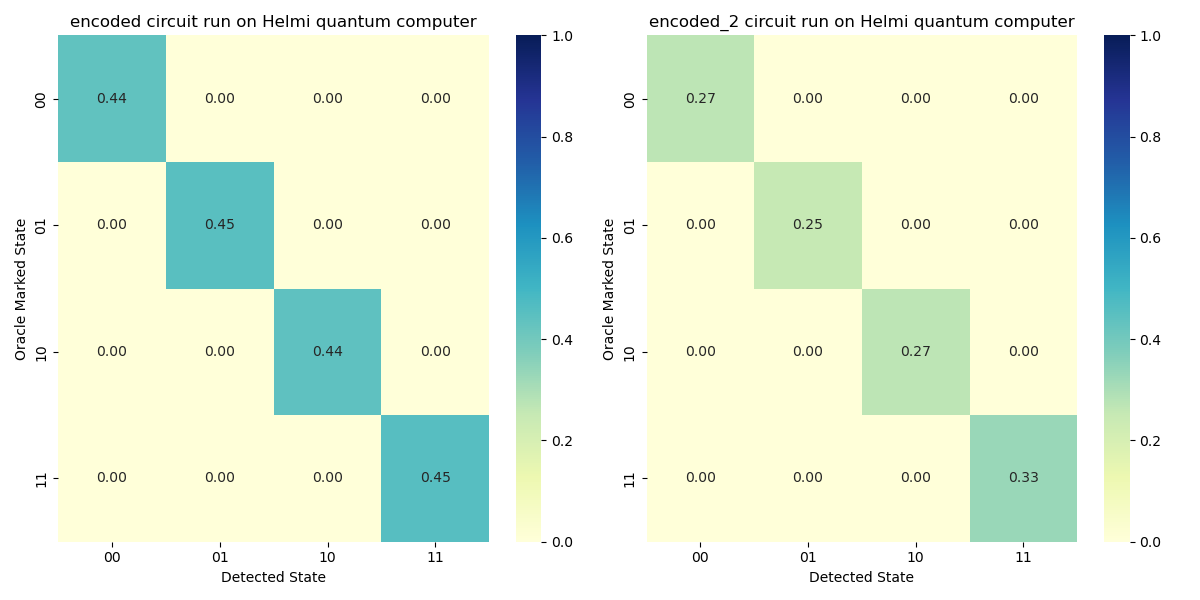
Figure 6. Accuracy for Grover’s search algorithm for different oracle marked state on Helmi QPU for both circuit version 1 (left) and version 2 (right).

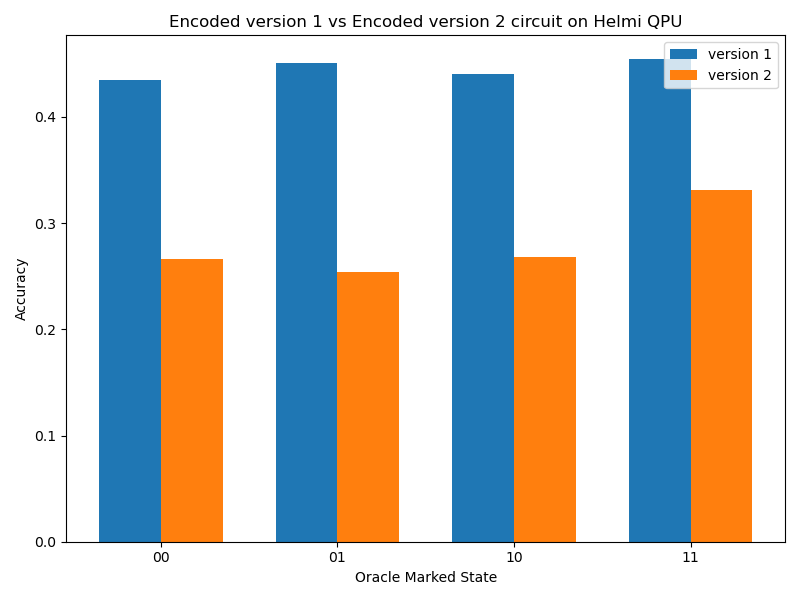
Figure 7. Performance comparison of Circuit 1 and Circuit 2 on Helmi QPU.

Notebooks

The Jupyter Notebook with the codes used in this post can be found here. They can be executed directly on the FiQCI infrastructure.

Conclusion

Qubit connectivity plays a crucial role in the performance and efficiency of quantum circuits across various quantum computing architectures. By carefully considering and optimizing qubit layout, especially in superconducting quantum computers like our Helmi QPU, we can significantly enhance the execution of quantum algorithms. The example of the encoded Grover’s search algorithm demonstrates that tailored circuit design, aligned with the specific connectivity model of a QPU, is essential for achieving optimal performance. This demonstrates that thoughtful design can maximize the usability and effectiveness of today’s quantum systems, even before we reach fault-tolerance.

Optimizing circuit design can be rather cumbersome. Tools and methods for automatizing the process are being developed, however. To mention a few, topology-aware optimization tools, such as the TopAs are being developed [13], and reinforcement learning for improving the circuit transpiling process have been explored [14]. This is one of the fields where we can expect AI for QC to make a notable impact.

References

1. S. Richer and D. DiVincenzo, “Circuit design implementing longitudinal coupling: A scalable scheme for superconducting qubits,” Phys. Rev. B, vol. 93, p. 134501, Apr. 2016. https://journals.aps.org/prb/abstract/10.1103/PhysRevB.93.134501

2. J. M. Gambetta, J. M. Chow, and M. Steffen, “Building logical qubits in a superconducting quantum computing system,” npj Quantum Information, vol. 3, no. 1, Jan. 2017. http://dx.doi.org/10.1038/s41534-016-0004-0. DOI: 10.1038/s41534-016-0004-0

3. Y. Zhao et al., “Realization of an Error-Correcting Surface Code with Superconducting Qubits,” Phys. Rev. Lett., vol. 129, p. 030501, Jul. 2022. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.129.030501

4. T. Strohm et al., “Ion-Based Quantum Computing Hardware: Performance and End-User Perspective,” arXiv, 2024. https://arxiv.org/abs/2405.11450

5. Y. Wan et al., “Ion Transport and Reordering in a 2D Trap Array,” Advanced Quantum Technologies, vol. 3, no. 11, May 2020. http://dx.doi.org/10.1002/qute.202000028. DOI: 10.1002/qute.202000028.

6. A. Bermudez et al., ““Assessing the Progress of Trapped-Ion Processors Towards Fault-Tolerant Quantum Computation,” Physical Review X, vol. 7, no. 4, Dec. 2017. http://dx.doi.org/10.1103/PhysRevX.7.041061. DOI: 10.1103/physrevx.7.041061.

7. C. Vigliar et al., “Error-protected qubits in a silicon photonic chip,” Nature Physics, vol. 17, no. 10, pp. 1137–1143, Sep. 2021. http://dx.doi.org/10.1038/s41567-021-01333-w. DOI: 10.1038/s41567-021-01333-w.

8. J. E. Bourassa and R. N. Alexander et al., “Blueprint for a Scalable Photonic Fault-Tolerant Quantum Computer,” Quantum, vol. 5, p. 392, Feb. 2021. http://dx.doi.org/10.22331/q-2021-02-04-392. DOI: 10.22331/q-2021-02-04-392.

9. J. Mower, N. C. Harris, G. R. Steinbrecher, Y. Lahini, and D. Englund, “High-fidelity quantum state evolution in imperfect photonic integrated circuits,” Phys. Rev. A, vol. 92, no. 3, p. 032322, Sep. 2015. https://link.aps.org/doi/10.1103/PhysRevA.92.032322. DOI: 10.1103/PhysRevA.92.032322.

10. L. Henriet et al., “Quantum computing with neutral atoms,” Quantum, vol. 4, p. 327, Sep. 2020. http://dx.doi.org/10.22331/q-2020-09-21-327. DOI: 10.22331/q-2020-09-21-327.

11. A. Browaeys and T. Lahaye, “Many-body physics with individually controlled Rydberg atoms,” Nature Physics, vol. 16, no. 2, pp. 132–142, Jan. 2020. [Online]. Available: http://dx.doi.org/10.1038/s41567-019-0733-z. DOI: 10.1038/s41567-019-0733-z.

12. B. Pokharel and D. A. Lidar, “Better-than-classical Grover search via quantum error detection and suppression,” npj Quantum Inf., vol. 9, no. 1, Mar. 2023. https://www.nature.com/articles/s41534-023-00794-6

13. M. Weiden, J. Kalloor, J. Kubiatowicz, E. Younis, and C. Iancu, “Wide Quantum Circuit Optimization with Topology Aware Synthesis,” arXiv preprint arXiv:2206.13645, 2022. https://arxiv.org/abs/2206.13645

14. D. Kremer, V. Villar, H. Paik, I. Duran, I. Faro, and J. Cruz-Benito, “Practical and Efficient Quantum Circuit Synthesis and Transpiling with Reinforcement Learning,” arXiv preprint arXiv:2405.13196, 2024. https://arxiv.org/abs/2405.13196